#lctp2023.031001#

本文作者：常景程、何洋，指导老师：刘玉孝

摘要：时空的维度一直是理论物理学家们感兴趣的话题。在古典物理中空间是三维的，任何物体都有属于其自身的空间坐标，其运行规律遵从牛顿三大定律。而时间就像一条长长的河流，独立于任何事任何人，始终向前流逝。当Einstein如上帝指引一般将时间维度与空间维度融为一体后，物理学开始有了惊人的发展。从狭义相对论到广义相对论，从额外维到弦理论，从全息原理到AdS/CFT对偶等等这一切都为量子引力理论和大统一理论进行了尝试和铺垫。

一、量子引力与AdS/CFT对偶  

    奇点的存在表明广义相对论对时空的描述仍然存在一些局限性。广义相对论中，物质和时空相互作用——“物质告诉时空如何弯曲，时空告诉物质如何运动”，但是物质的量子性与时空的经典特性相互不协调，而黑洞熵和黑洞热力学的提出更是表明时空需要更精细、更微观的描述，因此引力量子化开始成为了物理学界的重要课题之一。

    建立完整的量子引力理论是现代理论物理学家们追求的终极目标之一。1997年Maldacena提出的AdS/CFT对偶[1]打开了全息对偶¹的大门，让人们开始对量子引力有了进一步的理解和新的研究道路。2006年Ryu 和Takayanagi提出Ryu-Takayanagi公式[2]，进一步验证了AdS/CFT对偶并使得共形场论中纠缠熵的计算大为简化。Ryu-Takayanagi公式是指场论中AB两个子系统间的纠缠程度可以由更高一维时空中的余二维极小曲面的面积来度量，如图一所示。

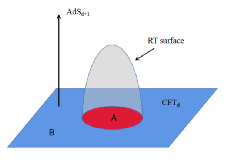
图一：Ryu-Takayanagi 面。

二、Jackiw-Teitelboim二维量子引力和黑洞信息悖论

    量子引力中Jackiw-Teitelboim引力[3][4]作为一个二维量子引力玩具模型，它的引力路径积分精确可解，近几年被人们广泛研究。随着人们对Jackiw-Teitelboim引力的深入研究，发现其正好是场论中Sachdev-Ye-Kitaev 模型[5]的低能有效对偶引力理论[6]，这极大地推动了量子引力方面的相关研究。正是由于其可精确计算的性质，Jackiw-Teitelboim引力也被用来研究黑洞信息悖论问题。

    黑洞信息悖论问题是指随着黑洞蒸发殆尽，我们是否可以恢复掉入黑洞的初始信息。Hawking的计算表明无法恢复这些信息，但Hawking的学生Page对此抱有疑问，他提出可用场论中纠缠熵的概念来度量黑洞蒸发过程中黑洞视界内外两部分系统之间的纠缠程度[7]。如果我们能够精确地计算一个蒸发黑洞的纠缠熵，那么就可以验证黑洞信息是否守恒。但是在经典引力中，纠缠熵几乎无法计算，而Jackiw-Teitelboim引力简单可解的性质导致其经常被用来研究蒸发黑洞的纠缠熵。

三、Karch-Randall 膜世界模型  

    也许我们的宇宙不仅仅是三个空间维度加一个时间维度，时空可能还有更多的维度，只不过局限于探测手段，我们还没有探测到这些额外的维度。Einstein提出广义相对论后，科学家们对额外维的探索从上个世纪二十年代的五维Kaluza-Klein理论开始一直到现在都未曾停止。在这一过程中，L. Randall和R. Sundrum两人1999年建立了卷曲的膜世界模型[8][9]，非常完美的解决了标准模型中的规范层次问题²，并在膜上实现了牛顿引力势。膜世界图像是指我们生活在五维AdS时空中的一张四维膜上，物质场被束缚在膜上，而引力可以在额外维中传播。2001年A. Karch和L. Randall对此做了进一步推广，考虑四维膜为AdS膜，提出Karch -Randall膜世界模型[10]。

    在Karch -Randall膜世界模型中，五维体时空具有两个边界，一个是时空的渐进无穷远边界，另一个是四维AdS膜，如图二所示。

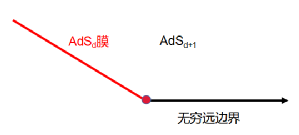
图二：Karch -Randall膜世界模型。

    Karch-Randall膜世界模型近几年来也常常被用来研究黑洞信息悖论问题。假设膜上有一个蒸发的黑洞，那么根据上文提到的Ryu-Takayanagi公式，其纠缠熵就可以由更高一维时空中对应的Ryu-Takayanagi 面的面积给出，见图三。

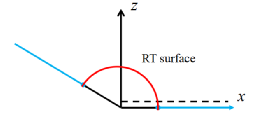
图三：膜世界全息中的Ryu-Takayanagi面。

四、楔形全息和二维量子引力的实现  

    在Karch -Randall膜世界模型中，考虑（d+1）维体时空内存在两张AdS_d膜，且这两张膜相交于同一个边界，构成一个楔形（见图四）。

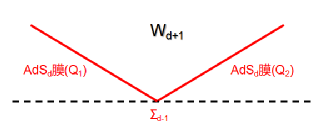
图四：楔形全息

    现在体时空的边界由这两张膜组成。对这样一个模型，T. Takayanagi等人提出了一种余二维的全息对偶理论——楔形全息[11]：

    楔形时空（W_d+1）中的经典引力和楔角（Σ_d-1）上的余二维的共形场论对偶。

    如图五所示，在楔形全局AdS₃时空中存在两个楔角，分别为红点和蓝点所处位置。基于楔形全息，通常用体时空内Ryu-Takayanagi面的面积来度量红蓝两点间的纠缠熵。

图五：全局AdS时空。图中绿色线是Ryu-Takayanagi面，两条黑色线为两张Karch -Randall膜。

    但是计算结果表明，此时有无穷多个Ryu-Takayanagi面，这使得对应的纠缠楔无法定义。为避免这个问题，2022年11月29日发表于Physical Review Letters的文章“Jackiw-Teitelboim Gravity from the Karch-Randall Braneworld”[12]通过考虑楔形时空中两张膜的涨落并对额外维进行约化，从Karch-Randall膜世界模型推导出了Jackiw-Teitelboim引力，而Jackiw-Teitelboim引力的动力学效应完美的解除了上述Ryu-Takayanagi面的简并性，使得只有唯一的Ryu-Takayanagi面来度量图五中红蓝两点间的纠缠熵。

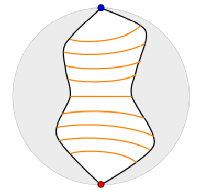
图六：考虑膜的涨落的AdS时空。图中黄色线为Ryu-Takayanagi面。

    见图六，从三维体时空角度来看，当我们考虑膜的涨落后，此时体时空内只有最中间的橙线最短，其长度正比于红蓝两点间的纠缠熵大小。这样就解除了图五中Ryu-Takayanagi面的简并性。

五、总结  

    Jackiw-Teitelboim引力的很多有趣性质使得其具有很重要的研究意义，而Karch -Randall膜世界模型也随着黑洞信息丢失问题的进展而广受关注。H. Geng等人从Karch -Randall膜世界模型出发，考虑了体时空中两张膜的涨落，最终通过额外维约化自然地实现了Jackiw-Teitelboim引力，不仅解决了楔形全息中Ryu-Takayanagi面的简并问题，也再一次让人们认识到了额外维与膜世界的重要性。

1、 AdS/CFT对偶是指一个d+1维AdS时空中的引力理论可以由一个d维的共形场论来描述。全息对偶简单来说就是我们生活的真实宇宙可能是由低一维的量子理论描述的——万物皆量子。

2、规范层次问题：电弱能标  与普朗克能标  有着巨大的差异，是标准模型中的重大疑难问题。

参考文献：

[1]J. Maldacena, Int. J. Theor. Phys. 38 (1999) 1113-1133.

[2]S. Ryu and T. Takayanagi, Phys. Rev. Lett. 96, 181602(2006).

[3]R. Jackiw, Nucl. Phys. B 252, 343–356 (1985).

[4]C. Teitelboim, Phys. Lett. B 126, 41–45 (1983).

[5]J. Maldacena and D. Stanford, Phys.Rev.D 94 (2016) 10, 106002.

[6]P. Saad, S. H. Shenker, and D. Stanford, arXiv: 1903.11115.

[7]D. N.Page, Phys. Rev. Lett. 71, 3743–3746 (1993).

[8]L. Randall and R. Sundrum, Phys. Rev. Lett. 83, 3370–3373 (1999).

[9]L. Randall and R. Sundrum, Phys. Rev. Lett. 83, 4690–4693 (1999).

[10]A. Karch and L. Randall, J. High Energy Phys. 05 (2001) 008.

[11]I. Akal, Y. Kusuki, T. Takayanagi, and Z. Wei, Phys. Rev. D 102, 126007 (2020).

[12]H. Geng, A. Karch, C. Perez-Pardavila, S. Raju, L. Randall, M. Riojas, and S. Shashi, Phys. Rev. Lett 129(2022)23, 231601.